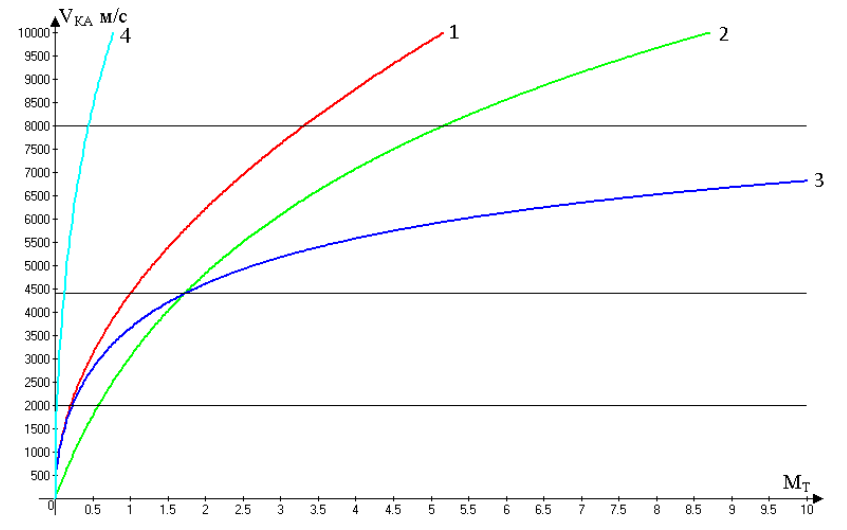
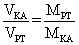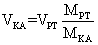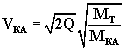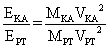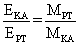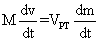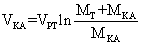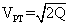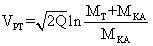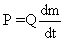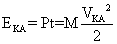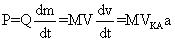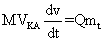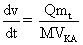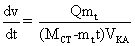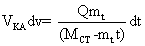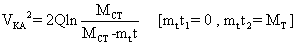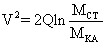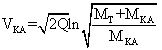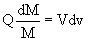Энергетические основы космического старта. Краткое содержание В работе предлагается сравнительный анализ энергетической эффективности трех основных способа запуска космического аппарата  с поверхности Земли. Ключевые слова: электромагнитная катапульта, пушка, ракета, авиационно-космическая система, ГПВРД. Таблица символов • КА  –  космический аппарат • РТ – рабочее тело, от которого отталкивается космический аппарат • М_КА – собственно масса космического аппарата, или конечная масса аппарата без топлива. • М_РТ – масса рабочего тела • М_Т – масса топлива • М_СТ – стартовая масса, М_СТ = М_КА + М_Т • М – текущая, переменная, масса космического аппарата в данный момент времени • m_t – удельный по времени расход топлива, кг/с • V_КА– скорость космического аппарата • V_РТ – скорость рабочего тела • V_Е – скорость истечения реактивной струи • V – скорость космического аппарата в данный момент времени • t – текущее время • Q – теплотворная способность топлива, Дж / кг • Е_РТ - кинетическая энергия рабочего тела • dv – дифференциал скорости • dm – дифференциал массы • dt – дифференциал времени • dv/dt = a  – изменение скорости КА • dm/dt = m_t  – изменение массы КА, эквивалентное удельному расходу топлива • Р – мощность двигателя • АКС – авиационно-космическая система • ГПВРД – гиперзвуковой прямоточный воздушнореактивный двигатель • ПВРД - прямоточный воздушнореактивный двигатель • ТРД – турбореактивный двигатель • I_у  – удельный импульс, отношение тяги двигателя к удельному расходу топлива Для того, что бы понять некоторые особенности  космического старта, интересно рассмотреть три способа запуска с Земли КА. Будем считать, что в качестве источника энергии используется условное топливо с одинаковой теплотворностью Q, его потенциальная  энергия переходит в кинетическую энергию аппарата согласно предлагаемым математическим моделям, а гравитационные, аэродинамические и любые другие потери  отсутствуют. Начальная скорость КА равна нулю. Возможны следующие варианты. 1. Рабочее  тело, и топливо, источник энергии находится за бортом КА. Это может быть электромагнитная катапульта, артиллерийское орудие (пушка), или скажем некий космический лифт. Рабочим телом в данной ситуации является Земля, с которой связаны данные устройства, источник энергии обычно также находится на Земле. Будем считать, что это топливо массой М_Т. Из закона сохранения  импульса получается  отношение величин получаемых  скоростей:                              (1)   или                            (2)   Так как масса РТ (Земли) намного порядков больше массы КА, то ее скорость после выстрела будет близка к нулевой.  Подставляя в отношение кинетических энергий, получаемых   Землей и  КА значение V_КА из (2) получаем:                                   (3)  →                            (4)   Это означает, что здесь практически всю энергию получает КА. Теперь можно вывести зависимость скорости КА от потраченного топлива:                                      (5) Отсюда можно посчитать минимальную стоимость вывода груза на околоземную орбиту. Если первая космическая скорость равна 7,8 км/с, а средняя стоимость электроэнергии 0,1$ за кВт-час (США), то получается примерно 1$ / кг. 2. Рабочее  тело и топливо (в данном случае РТ обычно и есть топливо) находятся на борту КА, что реализовано в ракетах. Возможна  передача энергии извне, например с помощью электромагнитного или лазерного излучения. Но в этом случае все равно с РТ связано определенное количество поглощаемой энергии, что позволяет говорить о его условной «теплотворной способности» как топлива. Из дифференциального уравнения для материальной точки переменной массы получается известная формула реактивного движения:                                 (6)  →                                 (7)      Если считать, что  вся энергия  топлива переходит в кинетическую энергию реактивной струи, то ее скорость  истечения определяется из удельной теплоты сгорания топлива Q                            (8)   →                                             (9) 3. Рабочее тело находится за бортом КА, а топливо, источник энергии, на его борту, например, в авиакосмических системах, где КА отталкивается от воздуха атмосферы, в артиллерийском орудии, где снаряд ускоряется за счет донного газогенератора. Возможен также некий гипотетический «левитатор», где КА отталкивается от Землю с помощью например магнитного поля. Как и в первом случае будем считать, что масса РТ намного  больше массы КА. Топливо после использования выбрасывается за борт, то есть, скорость истечения топлива равна нулю. Как и в первом случае энергию в основном получает КА с топливом на борту, а не рабочее тело. Будем считать, что  расход топлива dm/dt постоянная величина, а  мощность двигателя  P определяется расходом топлива, а работа, совершаемая двигателем, переходит в кинетическую:                    (10)                                                 (11)      Дифференцируя левую часть уравнения  (11)  по времени, а правую по скорости, получаем Pdt = M V_КА dv  (12)  или                                                       (13)  Можно заметить, что в отличие от реактивного движения, при постоянном ускорении  потребляемая мощность двигателя должна быть прямо пропорциональна  скорости КА относительно Земли (или неподвижного воздуха атмосферы).  При постоянном расходе топлива получаем зависимость массы КА от времени и следующие дифференциальные уравнения: М = М_СТ - m_tt  (14)                                 (15)  →                            (16) →                                                                                                    (17)   →                                           (18)  Интегрируя (18) получаем:                                                                  (19)  или                                 (20)  или                                               (21) Уравнение (21) похоже на формулу реактивного движения с одним отличием – появляется корень квадратный от лонарифма от соотношении масс. Что, как будет показано позже, приводит к важнейшим последствиям. Это же уравнение можно получить из дифференциального уравнения,  где расход энергии топлива (связанного с уменьшением веса аппарата) приводит к приращению кинетической энергии КА Qdm = MVdv  (22)  →                               (23)  Теперь можно построить зависимости V_КА  от  М_Т   для всех трех случаев. Для условного топлива предложим  значение  Q = 9 680 000 Дж/кг. Это составляет 72% от идеальной теплотворной способности кислород-водородного топлива.  Это соответствует значению скорости истечения реактивной струи V_Е = 4400 м/с из формулы (8), что характерно для кислород-водородных реактивных двигателей. Примем  M_КА = 1 . 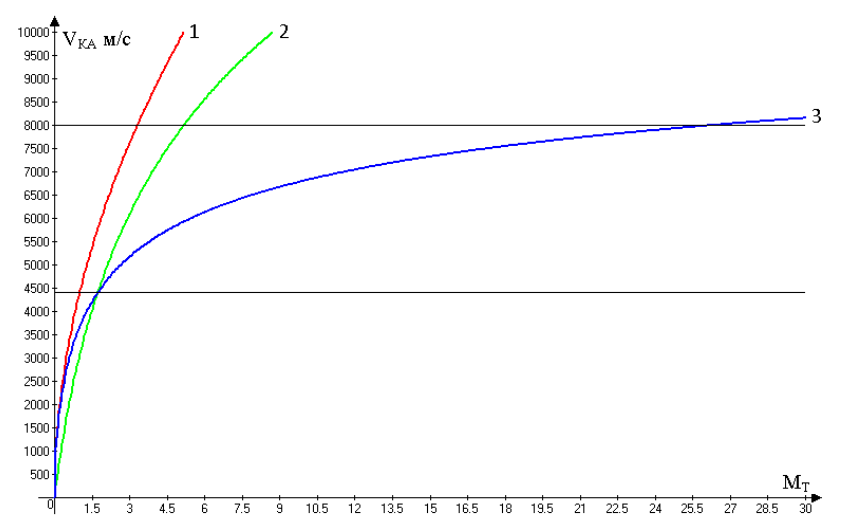Тогда М_Т  будет выражаться в относительных  единицах.  Результат для случаев 1, 2 и 3  представлен  схематически на рис.1 : Рис.1  Зависимость V_КА (м/с) от  M_Т  для трех разных способов старта. Видно, что характер кривых 1 и 3 на скорости менее 3000 м/с почти совпадают, и здесь реактивное движение (кривая 2) оказывается намного более энергозатратно. Например, для достижения 2000 м/с для КА М_Т = 0,2 в случае 1 и 3, М_Т=0,6 для случая 2. Затем картина кардинально меняется. Для достижения скорости 8000 м/с  в первом случае  М_Т = 3,3 , во втором М_Т = 5,2 , в третьем М_Т = 26,3 . Это конечно идеализированные данные. Тем не менее, они позволяют понять одну важнейшую особенность отличия чисто реактивного движения от случая 3. А именно,  любой КА, который несет топливо на борту и отталкивается от Земли или ее атмосферы, менее эффективен чем ракета на скорости V_КА > V_Е , в данном случае 4400 м/с (13 Махов).   Из-за того, что  само топливо в такой системе становиться балластом, что кажется парадоксом. Оно здесь расходуется уже не так рационально, как в случае реактивного движения. В случае АКС это ограничение преодолевается тем, что самый «тяжелый» его компонент, кислород, берется из атмосферы. Например, если считать источником энергии на борту КА водород, то теплотворность условного топлива будет в 9 раз больше: Q = 87 120 000 Дж/кг (Рис.2, кривая 4). Рис.2