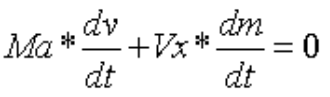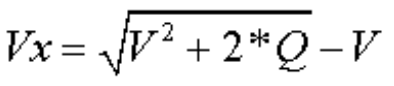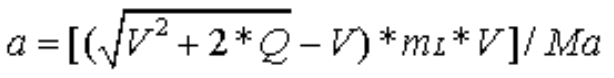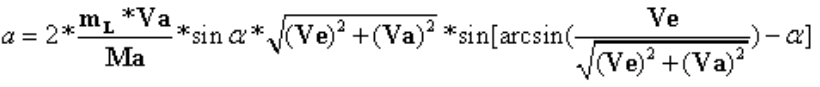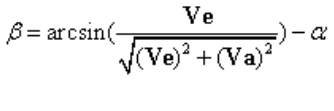Расчетные модели ускорителя с распределенным вдоль ствола топливом
1.
Модель падающего на клин газа (ударно-волновой ускоритель).
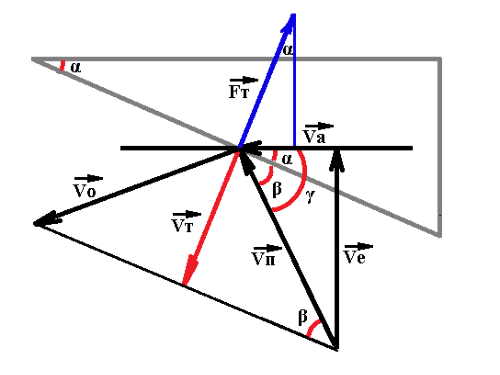
Рассмотрим математическую модель движения клина с углом раствора α , в которой газ от сгоревшего топлива падает на его наклонную
стенку со стенки ускорителя, ортогонально его движению со скоростью Ve. Топливо распределено вдоль стенки ускорителя с постоянной
плотностью mL = M/L, где M это масса всего топлива, а L длина ускорителя Понятно, что угол падения газов на стенку клина со
скоростью Vп будет отличаться от прямого угла, и будет зависеть от скорости аппарата Va. Примем, что газ испытывает упругое
отражение от стенки клина. То есть, меняется полный импульс газа, равный удвоенному произведению массы отраженного газа на
изменение вектора скорости Vт. Стенка клина испытывает давление с силой Fт = 2*mL* Va* Vт, где произведение mL *Va есть
количество отраженного топливо, его масса в единицу времени - расход толива. Ясно, что он будет пропорционален скорости
аппарата. Ускорение аппарата массой Mа тогда составит a = (2*mL* Va* Vт*sinα)/Mа. Из тригонометрических отношений находим
Vт = Vп*sinβ , а Vп = ( (Ve)2 + (Va)2 )1/2 , β = γ – α ,
γ = arcsin(Ve/( (Ve)2 + (Va)2 )1/2 .
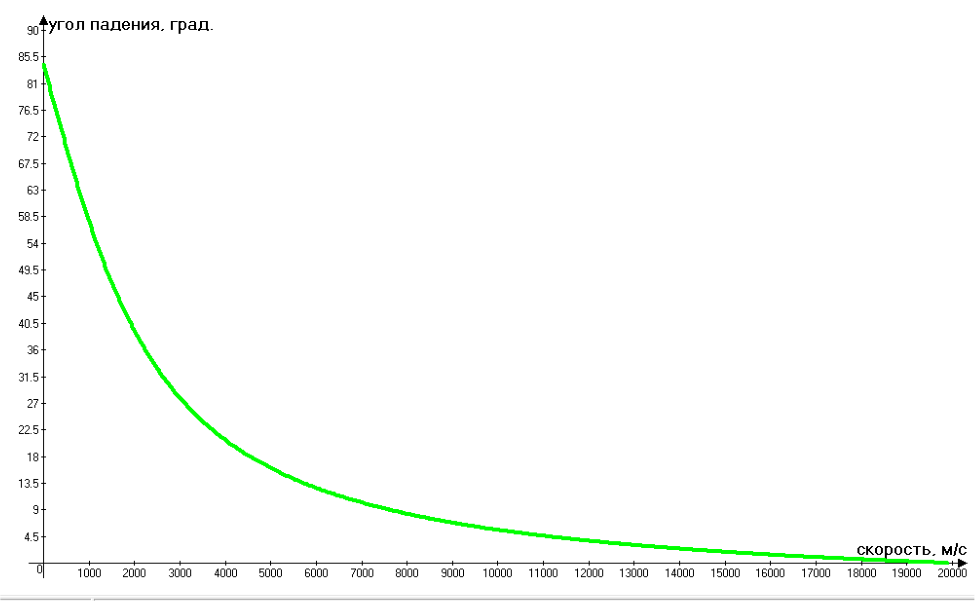
откуда зависимость угла падения газов на плоскость клина от скорости аппарата находится как:
А ускорение аппарата а как функция скорости Va
Получающийся интеграл правой части по dVa имеет слишком сложную форму в аналитическом выражении, чтобы им можно было
воспользоваться для нахождения скорости и пройденного пути аппарата в зависимости от времени. Поэтому, для их нахождения был
использован численный метод, где шаг времени для вычислений брался 0,01 секунды. Чтобы на старте поступающая масса mL* Va не
была нулевой, начальная скорость полагается 1 м/с. Угол клина α принимается 5.74o с тем расчетом, чтобы его тангенс был равен 0,1.
Скорость истечения газов принимается Ve = 2000 м/с, масса аппарата 1 кг, плотность распределения заряда 0,052 кг/м (78 кг на 1500
метров). Принимая энергоемкость топлива 2 МДж/кг, можно подсчитать КПД устройства, в зависимости от скорости.
Зависимость угла падения газов на клин от скорости аппарата.
2.
Модель реактивного сопла (линейный реактивно-прямоточный двигатель, ЛРД).
Представим теперь, что устройство работает как реактивное сопло, топливо в которое поступает со стенок ускорителя. Тогда можно
воспользоваться дифференциальным уравнением Мещерского:
где Mа это масса аппарата, которая в данном случае постоянна, dv/dt это ускорение аппарата, Vx это скорость истечения газов из сопла,
dm/dt расход топлива, который связан со скоростью аппарата: dm/dt = mL* V , а скорость истечения газа Vx можно определить как
где V это текущая скорость аппарата, а Q это удельная теплотворность топлива (Дж/кг). Тогда, абсолютное значение ускорения аппарата
можно выразить формулой:
Также, как и в первом случае, примем плотность распределения заряда mL = 0,052 кг/м , массу аппарата Ма = 1 кг, энергоемкость
топлива Q = 2 МДж/кг, и произведем численные расчеты.
Результаты расчетов для двух моделей представдены ниже на графиках 1,2 и 3. На графике 2 добавлены зависимости скорости ЛА для
обычного реактивного движения и случая, когда рабочее тело находится за бортом ЛА, а топливо, источник энергии, на его борту
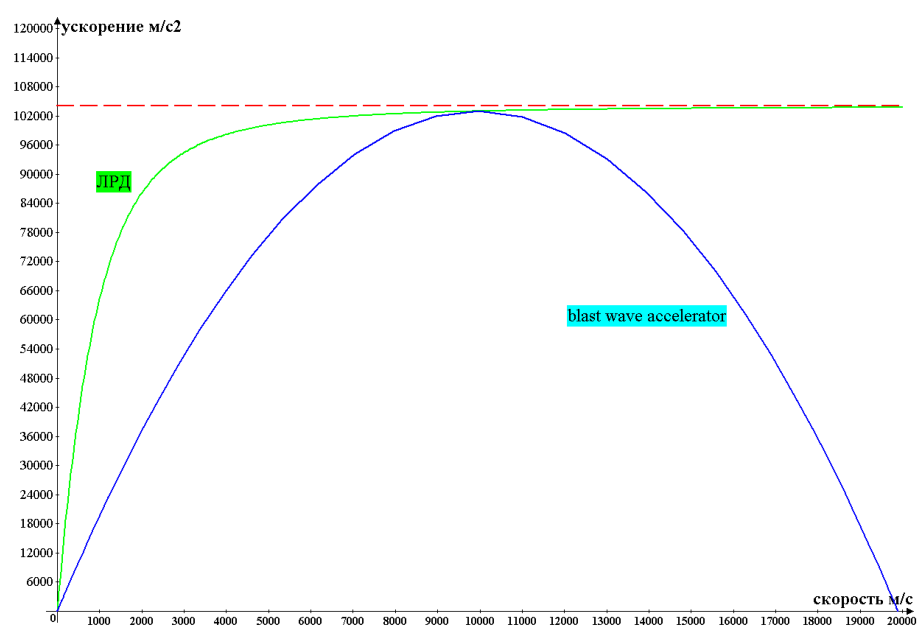
1. Зависимость ускорения аппарата от скорости:
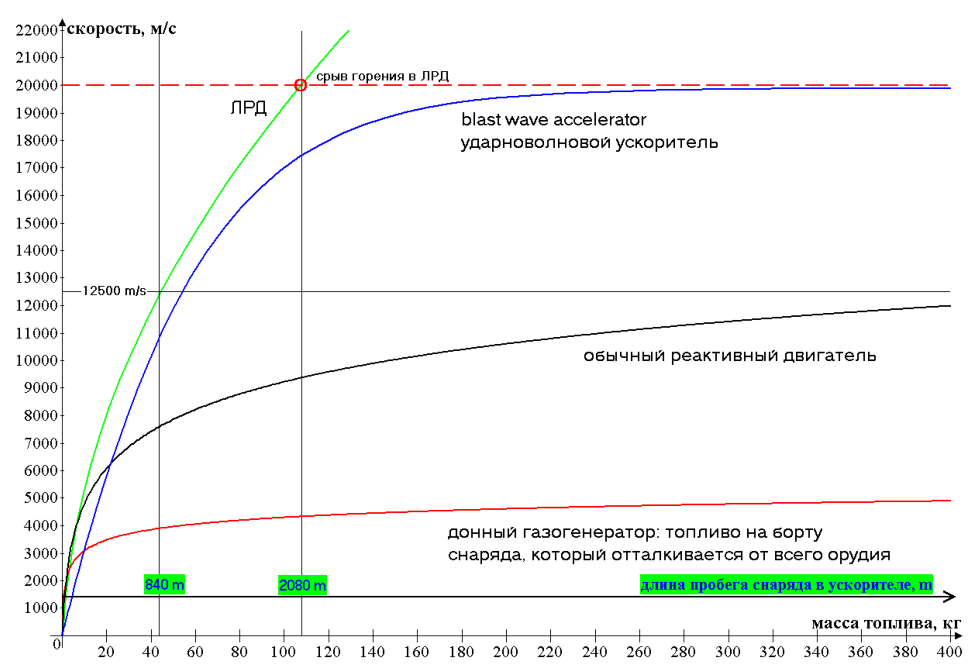
2. Зависимость скорости аппарата от от массы топлива / длины ускорителя.
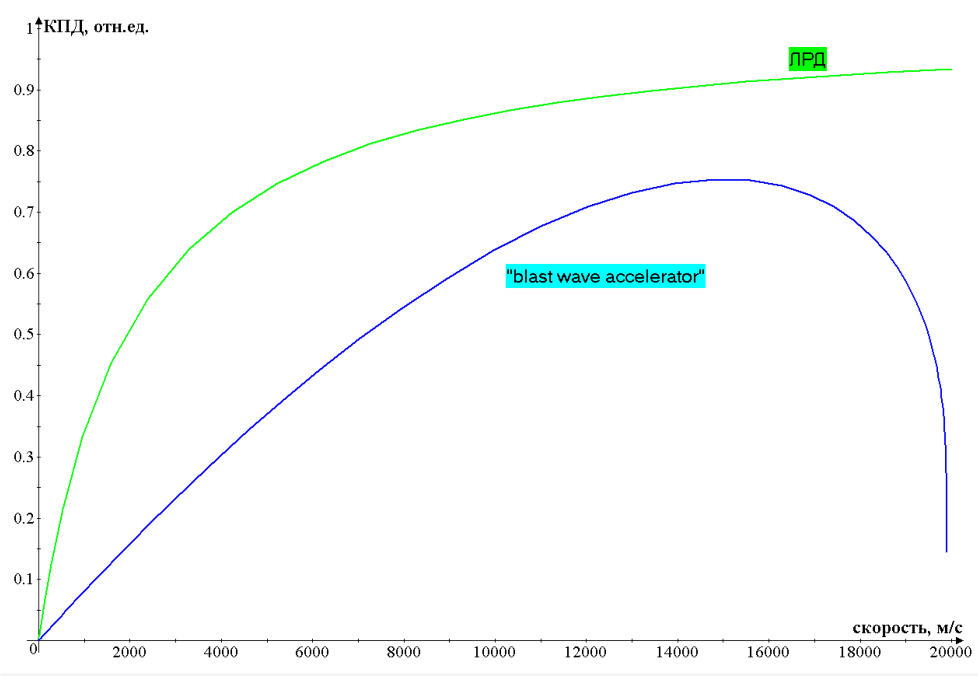
3. Зависимость КПД системы от скорости аппарата
Для вывода снаряда массой 1 кг с характеристической скоростью 12500 м/с нужно всего 43,6 кг пороха в случае ЛРД модели, и 54,5 кг в
случае ударноволновой модели. Так же, как и в работе [Войтенко], КПД ЛРД устройства растет вместе со скоростью, достигая 93%, а для
второй модели КПД достигает 75% при достижении скорости 15 000 м/с, а затем резко падает. Все это внушает оптимизм на предмет
создания подобных ускорителей, способных выстреливать снаряды со скоростью более 12500 м/с.